Building a Granular Synth in Swift, Part 7: Mixing Sounds
If you have been following along, you may have noticed that our volume drops as we increase density. Density means more grains are playing at once so this is rather counter-intuitive. I breezed past this issue at the outset, but let’s revisit it now. Maybe you noticed this line in the GrainSource struct:
let amplitude = 1.0 / Float(Grain.grainCount)When adding up the sound of 10,000 grains, there is the potential for our sound to be 10,000 times louder than the maximum allowed, resulting in distortion utter obliteration. Dividing the summed sample by the number of grains ensures that we will always stay within the allowable range, which, because we are representing sound with float, is -1 to 1. As the number of grains goes up, we turn down the volume accordingly. But why the drop in volume?
To understand this, let’s do a quick review of how sounds combine. In essence it’s quite straightforward: they are simply added together. What complicates this addition, however, is phase-cancellation. Phase is just a cool-sounding word for how the peaks and troughs of the sound waves line up in time. When two peaks line up, they add together, but when we run into a peak and a trough, they cancel each other. In digital audio, we simply sum together the samples at a given time step. When one is negative (a trough) it will cancel out (or reduce) a sample that is positive (a peak).
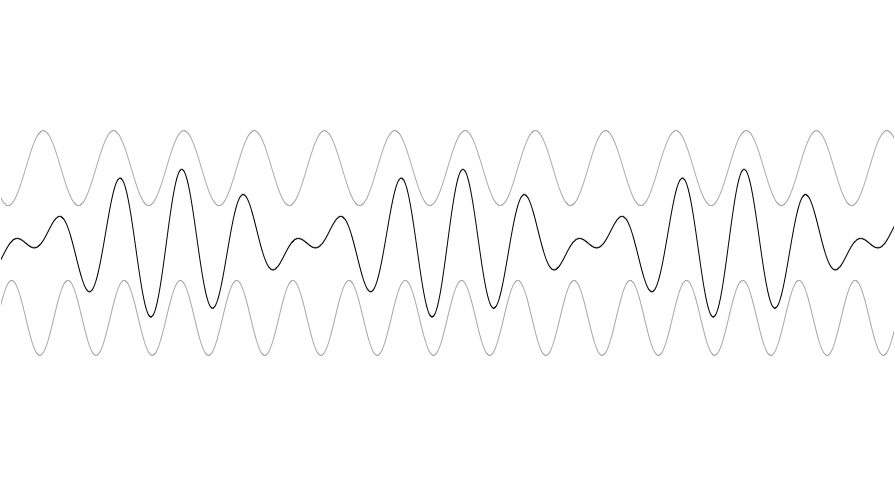
So, if we have two sounds that are lined up in time, with many of their peaks and troughs matching, i.e. highly correlated, summing them will potentially result in double their individual amplitudes. In this case dividing by the number of sounds, two, will get us right back to the amplitude we started with.
Of course in nature, there is no such division happening, and the sounds just add up. The problem here is that our electronics and speakers have limits on the amplitude they can reproduce, so to avoid distortion we have to maintain a given range.
In the case of our grains, as with most naturally occurring sounds, there is a lot of phase variation, i.e. the peaks and troughs do not line up, and tend to reinforce and cancel each other at random. When they occasionally do line up, you get phenomena like sonic booms and shattered glass.
Our question then becomes what is the expected amplitude when we add together a bunch of samples with random phases. Here the trig gets hairy, and my approach would be to just whip up a simulation and measure, as I find procedural code easier to grok than symbolic math. A nice discussion along these lines can be found at: Random sums of sines and random walks – God plays dice. The result is √(πN/4). The π/4 is about .79, which is a slight attenuation, but assuming our source samples aren’t super loud we can ignore that term and get good results with a simple √N.
let amplitude = 1.0 / sqrt(Float(Grain.grainCount))With this small tweak, the perceived amplitude doesn’t vary nearly as much when we increase density, and things sound as they should. Of course we will probably want to add a gain control soon too, to be able to control our volume explicitly, but for now the grain addition is nice and stable.